Research

The Psychometric Function (PF) relates some behavioral measure (e.g., proportion correct detection) to some task characteristic (e.g., stimulus intensity). Typically of interest is the 'threshold' stimulus intensity. The threshold is usually defined as that stimulus intensity at which observers reach a specific level of performance. Some suggest that, in order to obtain a threshold estimate which is as unbiased as possible, we should allow the upper asymptote of the PF or 'lapse rate' to vary during function fitting. In their influential paper, Wichmann and Hill (2001) claim that allowing the lapse rate to vary results in threshold and slope estimates which are 'essentially unbiased', seemingly irrespective of what stimulus placement regimen is used. In Prins (2012), I have attempted to replicate these results, but was unsuccessful. Instead, I obtained systematic and significant biases in both thresholds and slopes, especially when stimulus placement was controlled by an adaptive method. Prins (2012) discusses the origin of this bias and suggests a few strategies to circumvent this bias. Two of these strategies are currently investigated further in my lab and are mentioned below.

Concepts borrowed from the General Linear Model can be applied to the fitting of psychometric functions (PFs) and testing of research hypotheses. The Palamedes toolbox (Prins & Kingdom, 2009) implements these concepts into routines which allow the user to fit multiple PFs simultaneously to several datasets (arising for example, from different conditions in an experiment). 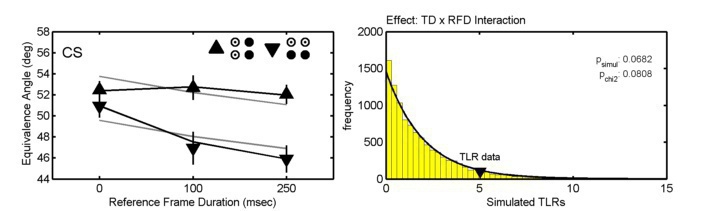The user is given considerable flexibility in constraining parameters in order to specify models. For example, the triangles in the example in the figure above show threshold estimates obtained in a factorial 2 x 3 experimental design by fitting the six conditions individually. The black lines in the figure show the threshold estimates when a model is fitted that allows thresholds to take on any value, but constrains the slopes to be equal among the six conditions (i.e., a single, shared slope estimate is derived for the six conditions), and also constrains the lapse rate to be equal among the six conditions (this is an 8 parameter model). The gray lines in the figure show a model in which thresholds are allowed to vary as a function of the three-level factor as well as the two-level factor but not their interaction (this is a 6 parameter model). Comparing these two models statistically amounts to testing whether the effects of the two factors interact significantly. The figure on the right shows that the interaction is 'marginally significant' (whatever that means) by the classical null hypothesis logic (specifically, the likelihood ratio test). By Akaike's Information Criterion the model which includes the interaction term is preferred over the model that does not. A goodness-of-fit test can be used to test whether a model provides a good fit (the model which includes the interaction does provide a good fit, by the way). Does this all provide some relief from the trouble caused by lapses (as promised above)? Yes: (1) current research in my lab shows that model comparisons such as these are very robust against violations of assumptions regarding the value of the lapse rate when a fixed value for the lapse rate is assumed and (2) multi-PF model fitting allows one to derive a single, more reliable and less-biased lapse rate from all data gathered by an observer. Data shown taken from Prins (2008).

Many surfaces are naturally textured. Modulations of the characteristics of such textures (such as changes in local orientation, spatial frequency, contrast, etc.) across visual space give us important information about the shape of the textured object or surface. Much is known about the mechanisms which extract local characteristics of the visual stimulus, such as orientation, spatial frequency, motion, etc. Much less, however, is known about how these local characteristics are combined to give rise to the perception of textured surfaces and how information regarding the shape of these surfaces is extracted.

Features of motions tokens (e.g., planarity, depth, color, size) other than their retinal location influence which solution to the correspondence problem in apparent motion is generated. This is generally taken to mean that either the solution to the correspondence problem is generated at a relatively high level of visual processing or that such token features may in fact be fundamental visual properties that are available at a relatively early stage of visual processing. However, effects of motion token characteristics other than their retinal position are found only when the retinal positions are in a relatively narrow range where the visual system is relatively indecisive based on retinal position alone (such as shown here). And even then, the effect is small (chances are that you see vertical motion above which compromises the chromatic integrity of the tokens). Also, I have shown that the effects of features other than the location of tokens in the retinal image exert their influence relatively slow. This suggests that correspondence matches between tokens are assigned by a mechanism that acts on retinal location. Only when no solution can be generated fast may a slower, attentive conscious process sway the solution based on whatever the observer feels would make a good match (researchers have shown effects of color, spatial frequency, depth, co-planarity, and even intention by experimenter's instruction).

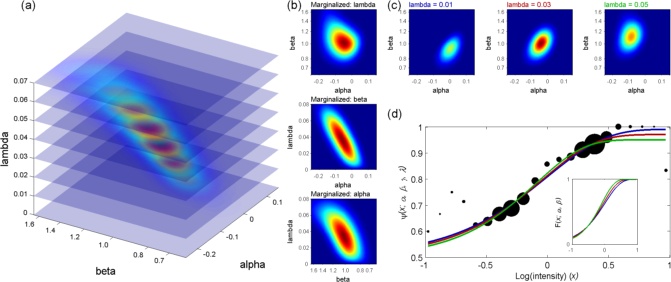
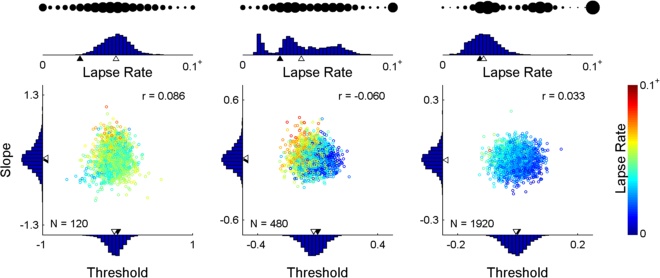
Many other possibilities exist. Example: If you care only about the threshold but you don't want to assume some fixed slope or lapse rate, marginalize both slope and lapse rate. In the simulated results below, everything was the same as above, except that the method marginalized slope and lapse rate, leaving as it's only goal reduction of the uncertainty in the threshold parameter. Note that the method changed its placement strategy and that the result is a more precise threshold estimate but a less precise slope estimate.

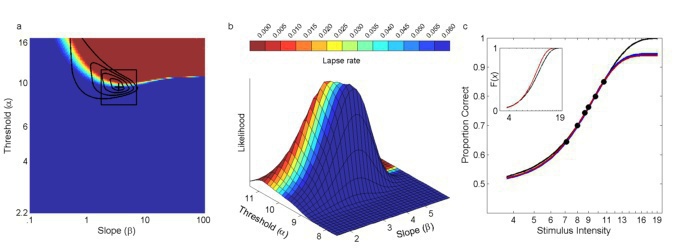
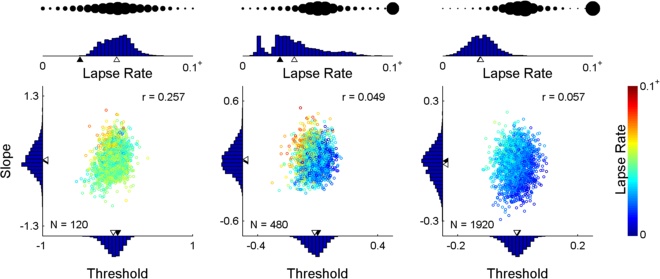
When an adaptive method is used to control stimulus placement, threshold and slope estimates may be subject to significant bias when the assumed fixed lapse rate does not match the generating lapse rate. When the lapse rate parameter is freed in a subsequent fitting procedure but was not targeted by the adaptive method, the (high) uncertainty in the lapse rate contributes to the uncertainty in threshold and slope [see (a) above, which shows the posterior for the most likely outcome of 960 trials placed in a manner typical of Kontsevich & Tyler's (1999) Psi-method]. Moreover, bias persists when we free the lapse rate and may even be exacerbated. When the lapse rate is explicitly targeted by the adaptive method, many trials are wasted on obtaining an accurate estimate of the (nuisance) lapse rate parameter. So, how do we give just the right amount of attention to the lapse rate? In Prins (2013), I propose we do this: We maintain a posterior distribution that includes the lapse rate [i.e., a posterior such as shown in (a) above] but we make it the explicit goal of the method to reduce uncertainty in the marginal threshold x slope distribution [that's the distribution in the top panel of (b) above]. The appeal of this strategy is that the method can (and will) target the lapse rate by placing stimuli at near asymptotic levels, but only if this is the best placement to reduce uncertainty in threshold and/or slope. I call this strategy the Psi-marginal method. Below are some parameter estimates resulting from 2,000 simulated runs controlled by the Psi-marginal method. The 'bubbles' up top indicate the method's choice of stimulus placement from performance near the low asymptote performance on the left to performance near the high asymptote on the right. Click here to download Matlab(tm) code that demonstrates the method.