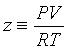
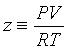
The simplest extension of the ideal gas equation is the virial equation, where the compressibility factor is assumed to depend on the pressure or the volume:
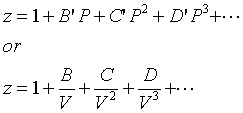
The coefficients B and B' are called the second virial coefficients, C and C', the third virial coefficients, and so on. In most applications, only the series is truncated after the first term. The predictions from the two truncated equations are slightly different. Smith, Van Ness and Abbott recommend the equation in terms of the pressure:
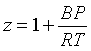
The older form is referred to as the Hougen-Watson generalized EOS. In this model, the third parameter is the critical compressibility factor. The second category of EOS is called the Lee-Kesler equation and uses the acentric factor as the third parameter. Like the critical properties, the acentric factor is a material property, different for different materials. The compressibility factor is then determined by:

where z0 and z1 depend on the reduced temperature and pressure. Values of these parameters are given in tabular form.
The virial equation can also be written in a "generalized" form, with the second virial coefficient given as a function of the acentric factor and the reduced temperature and pressure:
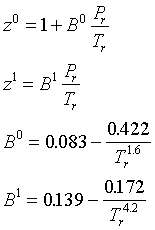
The generalized virial equation has the advantage of being easy to use, but it is of limited accuracy. Just as with the virial equation itself, it cannot represent the liquid phase. In addition, it is only an approximation to the Lee-Kesler equation for certain values of Pr and Tr. The region of applicability is indicated by Figure 3.15 in Smith, Van Ness and Abbott.
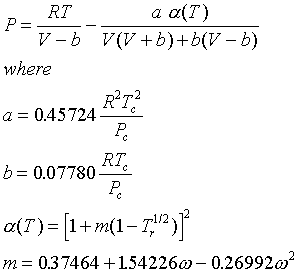
A similar equation is the Redlich-Kwong EOS:
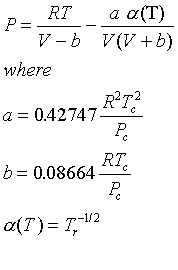
(Note that this is the same as the R-K equation given in the book, but it is written in a slightly different format.)
There are several modifications of these two. One of the more popular is the Soave-Redlich-Kwong (SRK) equation, which is the same as the RK except

Note that the PR and SRK equations are quite similar, and may be expected to give similar results.
These cubic equations are characterized by predicting three real values of the volume in the vapor-liquid region. The smallest volume is the liquid; the largest, the vapor. The intermediate value has no physical significance.
There are several modifications of both these equations to increase their range application. For example, the Peng Robin Stryjek Vera (PRSV) model uses a modified expression for the parameter, among other things. The simulator companies (Aspen, Simulation Science, Hyprotech) each have their suggested EOS model. Hyprotech recommends the PRSV model for most hydrocarbon and moderately non-ideal systems.
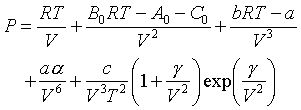
Unlike the previous models, there is no simple formula for the constants; each must be determined experimentally for each different material. In addition, the "constant"C0 is a function of temperature for many materials. Values of the constants for many hydrocarbons are given in Perry's.